Дефект веса
Рис. 1. Дефект массы.
Масса и энергия являются фундаментальными понятиями в теоретической физике. Масса, как количество материи и энергия, как свойство материи, совершать работу. Дефект массы, это понятие как исчезновения материи, является антинаучным.
Поскольку это явление установлено экспериментально, то речь может идти не о массе, а о весе, который может изменяться в зависимости от расстояния до тяготеющего тела или от силы притяжения к нему.
Поставим вопрос: равны ли силы гравитации при измерении массы одного и того же тела, находящегося целом и раздробленном состоянии?
Окунь утверждает: «В частности, ни у кого не вызывает сомнения, что масса вазы равна сумме масс ее осколков» [1].
m=∑·mn (1)
Безусловно, такое утверждение правильное, но если мы привяжемся к весу, то он будет расти по мере увеличивающегося количества частиц раздробления этой вазы. При
lim n→∞, вес p≠∑·mn
Одним из примеров может быть так называемый «дефект массы» деления атомных ядер. Наука в этом случае находит объяснение в том, что нуклоны в атомном ядре связаны между собой ядерными силами и для разделения ядер на протоны и нейтроны необходимо затратить энергию, эту энергию называют «энергией связи» [2]. В релятивистской механике масса не является аддитивной физической величиной, то есть масса системы в общем случае не равна сумме масс компонентов, а в классической механике сумма масс, составляющих тел, равна обшей массе системы. Но есть исключение из правил и в механике. Для этого нужно разбить вазу Окуня на мельчайшие частицы и убедиться в том, что при делении вещества его делимые части покажут больший вес. Что в этом случае происходит? Наука пока не дает однозначного и правильного ответа.
Казалось бы, какая разница ваза находится в первозданном виде или она разбита на отдельные кусочки. Этот пример привел как аналогию, на самом деле наши коммерческие весы покажут один и тот же вес. Но если вазу раздробить на пылевые частицы (до бозонов Хигса доходить не будем), и взвесить эту пыль на прецизионных весах в вакууме, то разницу можно обнаружить.
Что же все-таки происходит? А происходит следующее, при дроблении мы многократно увеличиваем поверхность вещества и его объем. Существует закономерность, которую заметил еще Г. Галилей, после чего был сформулирован Закон квадрата-куба. Данный закон звучит так: если увеличить линейный размер в n раз, его площадь поверхности увеличится в n² раз, объём – в n³ раз.
Где А1 – площадь поверхности исходной частицы (объекта), А2 – новая площадь поверхности, v1 – объем исходной частицы, v2 – новый объем, l1 – линейный размер исходной частицы (тела), l2 – новый линейный размер.
Из данного закона следует, что при увеличении размеров частиц их общий объем увеличивается быстрее, чем площадь поверхности.
В моем случае нужно решить противоположную задачу: нужно раздробить вазу на мелкие частицы. Из вазы получится очень много пыли и она может разлететься, поэтому заменим ее шариком из пластилина радиусом R. Поверхность данного шарика определяется по формуле.
S=4πR2 (2)
Разрежем данный шарик на два полушария, скатаем их в новые шарики и измерим их радиусы R1.
Поверхность одного шарика будет равна:
Поверхность двух шариков
Вновь разрежем на половинки, полученные шарики и скатаем их, получим 4 шарика и так далее до бесконечности.
Чтобы не утомлять читателя кухонной процедурой найдем поверхность одного шара Sn1 на n-ном делителе.
Где R – радиус первоначального шара, n – количество частиц (шариков).
Найдем общую поверхность шариков.
Глядя на приведенные преобразования можно заключить, что при делении первоначального объекта на бесконечное количество, его поверхность многократно увеличивается. При этом, казалось бы, объем остается прежним, на самом деле объем также растет, т.к. мелкие шарики невозможно упаковать плотно из-за промежутков между ними.
Отсюда можно сделать вывод: с большей поверхностью (объемом) взаимодействует большее количество красных фотонов (крафонов), гравитонов земли. В данном случае я имею в виду не загадочные и неуловимые наукой гравитоны, а реальные красные (инфракрасные) фотоны, вылетающие из земли и окружающего пространства, отвечающие за гравитационное взаимодействие. Получается, что при одном и том же количестве (в среднем) крафонов земли, вероятность попадания в большую поверхность (объем) увеличивается, тем самым увеличивается сила притяжения, соответственно, вес.
Вот здесь проявляется тот самый феномен квантованности гравитации. В данном случае можно сказать, что в классической механике возникает дефект веса, а не массы.
Это говорит о том, как такового дефекта масс нет, а присутствует увеличение общей поверхности тел при их многократном дроблении. Соответственно, при конечном количестве крафонов земли, вылетающих в единицу времени, возникает соответствующая сила притяжения, т.е. соответствующий вес. Чем больше раздроблено тело, тем больше его поверхность, тем больше его вес.
Два тела, имеющие одинаковую массу (одинаковое количество атомов), но имеющие разный объем (плотность), будут иметь разный вес. Объемное тело будет иметь больший вес, благодаря тому, что его поверхность будет больше пронизана крафонами земли. Это и есть феномен квантованности гравитации.
Здесь я не учитываю выталкивающую силу Архимеда, которую учитывал Я. Перельман в своей книге [3].
Тонна дерева или тонна железа
Детский вопрос: что тяжелее килограмм ваты или килограмм железа? Обычно такие вопросы ставят школьники. В детских вопросах всегда есть скрытый подвох, который сходу многими не улавливается. В то же время в таких вопросах проглядывает некая очевидность для быстрого ответа. Обратимся к классику по детским вопросам Якову Перельману, который спрашивает: что тяжелее – тонна дерева или тонна железа?
Три ответа: 1) вес одинаковый, 2) тяжелее железо, 3) тяжелее дерево. Посмотрел ролики в интернете, почитал некоторые комментарии. Господа! Полнейшая разноголосица, три противоположных ответа и все правильные! Вот Перельман дает правильный ответ, но есть одно дополнение.
Приведу отрывок из книги.
«Общеизвестен шуточный вопрос: что тяжелее — тонна дерева или тонна железа? Не подумавши, обыкновенно отвечают, что тонна железа тяжелее, вызывая дружный смех окружающих.
Шутники, вероятно, еще громче рассмеются, если им ответят, что тонна дерева тяжелее, чем тонна железа. Такое утверждение кажется уж ни с чем не сообразным, — и, однако, строго говоря, это ответ верный!
Дело в том, что закон Архимеда применим не только к жидкостям, но и к газам. Каждое тело в воздухе “теряет” из своего веса столько, сколько весит вытесненный телом объем воздуха.
Дерево и железо тоже, конечно, теряют в воздухе часть своего веса. Чтобы получить истинные их веса, нужно потерю прибавить. Следовательно, истинный вес дерева в нашем случае равен 1 тонне + вес воздуха в объеме дерева; истинный вес железа равен 1 тонне + вес воздуха в объеме железа.
Но тонна дерева занимает гораздо больший объем, нежели тонна железа (раз в 15), поэтому истинный вес тонны дерева больше истинного веса тонны железа! Выражаясь точнее, мы должны были бы сказать: истинный вес того дерева, которое в воздухе весит тонну, больше истинного веса того железа, которое весит в воздухе также одну тонну.
Так как тонна железа занимает объем в 1/8 куб. м, а тонна дерева — около 2 куб. м, то разность в весе вытесняемого ими воздуха должна составлять около 2,5 кг. Вот насколько тонна дерева в действительности тяжелее тонны железа!» (Конец цитаты).
Перельман прав, но не совсем, в действительности тонна дерева будет весить в вакууме меньше. Он не уточняет в каком состоянии находилось дерево: сухое, только что спиленное. Дерево имеет волокнисто-капиллярную структуру строения древесины, в которой будет находиться воздух (дерево сухое), или вода. Если взвешивать, сравнивать вес в вакууме, то дерево потеряет этот воздух (жидкость) и для баланса веса придется добавлять гирьки.
Выталкивающую силу Архимеда Перельман учел, взвешивая и сравнивания веса в реальных атмосферных условиях. Атмосфера – это газ, который имеет определенную плотность, поэтому в соответствии с законом Архимеда, с учетом его балансировался вес двух разных тел.
Но Перельман не учитывал квантованности гравитации. Если дерево превратить в тонкодисперсный опил, то вес этих опилок будет еще больше, что и было доказано выше.
Для сравнивания результатов взвешивания железа и дерева их нужно поместить в вакуумную лабораторию (другую инерциальную систему отсчета), где и будет обнаружен дисбаланс, больший вес будет иметь древесная пыль.
Источники
- Окунь Л.Б., Понятие массы, Успехи физических наук, т. 158, вып. 3, 1989
- Дефект массы, Википедия / https://goo.gl/R5fxjx
- Перельман Я. И. Тонна дерева или тонна железа, Занимательная физика, книга1, гл.5 / http://allforchildren.ru/sci/perelman1-58.php



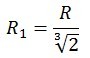
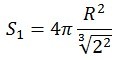
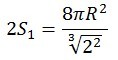
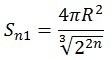
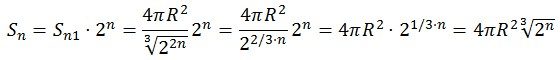




А давайте отнесёмся к гравитации как к закону Архимеда, но в 3-ёх мерном пространстве и как бы наоборот?;) Поясню, допустим всё же существование эфира. Пуанкаре скорее прав..
Помещение любого материального тела в эфир вызывает инвариантную выталкивающей Архимедовой силе притягивающую силу?;) Масса, количество занятого пространства в эфире.. С Вашей теорией переноса гравитации фотонами не могу согласится из-за сохранения гравитации при полном экранировании Э.М. излучения..? В моменты парада планет или солнечных затмений сила гравитации должна изменяться?;)
скорость света по-новому
«Помещение любого материального тела в эфир вызывает инвариантную выталкивающей Архимедовой силе притягивающую силу?;) Масса, количество занятого пространства в эфире.. С Вашей теорией переноса гравитации фотонами не могу согласится из-за сохранения гравитации при полном экранировании Э.М. излучения..? В моменты парада планет или солнечных затмений сила гравитации должна изменяться?;)»
—————————
В данном случае, не вдаваясь в тонкости гравитации, можно считать силу тяготения постоянной (инвариантной) только для покоящихся тел. Воздушную среду можно отдаленно сравнить с эфиром. От таких преобразований гравитационное взаимодействие не изменится, также как и противодействие Архимедовой силы.
Относительно Вашего несогласия переноса гравитации фотонами, парада планет и солнечных затмений.
Начну с солнечного затмения. Площадь тени, отбрасываемой Луной во время полного солнечного затмения S = 48,5 тыс. км2. Поверхность полушария Земли 255,05 млн. км2. Полутень от Луны занимает 0,019%. Каким образом Луна может воспрепятствовать гравитации Солнца. Кроме того, Луна в данном случае является неким ретранслятором, т.к. ее теневая сторона не охлаждена до абсолютного нуля.
Что касается парада планет, Вы можете рассмотреть тень от прохождения Венеры, а тем более Меркурия по диску Солнца без телескопа?
«скорость света по-новому»
—————————
Умственный эксперимент
Хорошо, а Лунное затмение?;)
«Хорошо, а Лунное затмение?;)»
—————————
Луна, она же не к Солнцу привязана. Поэтому даже те 108 мин., при максимальном затмении, которые бывают весьма редко, Луна не может изменить свою орбиту. При том, даже в фазе полного затмения Луна продолжает освещаться солнечными лучами (красная Луна), которые проходят по касательной к земной поверхности.
Порошок из любого материала имеет поверхность большую поверхности сплошной глыбы из него. К этой поверхности всегда «приклеиваются» молекулы воздуха (абсорбция) Так что порошок будет тяжелее. Вес же порошка же свежесрубленного дерева будет со временем уменьшаться, т.к. порошок будет сохнуть.
«Вес же порошка свежесрубленного дерева будет со временем уменьшаться, т.к. порошок будет сохнуть».
Лес рубят — щепки летят! Все щепки упаковываем в полиэтилен.
В ОТО нет явной или неявной связи между спином и видом метрики. Метрика определяется источниками поля — распределением масс и энергии. Обычная шварцшильдовская метрика без посторонних коэффициентов тоже ведь возникает в ОТО.
Hello. And Bye.
And to you bye
В общем с идеей автора абсолютно согласен, но в частных выводах по ходу повествования статьи при использовании таких общепринятых понятий, как объём, плотность, вес и масса тела — хотелось бы иметь (для лучшего восприятия) более полное разъяснение… Поясню: по ходу чтения всё абсолютно понятно и совершенно логично, но когда дело доходит до выводов … «Два тела, имеющие одинаковую массу (одинаковое количество атомов), но имеющие разный объем (плотность), будут иметь разный вес. Объемное тело будет иметь больший вес, благодаря тому, что его поверхность будет больше пронизана крафонами земли. Это и есть феномен квантованности гравитации.» начинают возникать вопросы. Объём — это линейные размеры тела, а плотность (в нашем случае) — количество атомов в единице объёма (например в 1м.куб.) данного тела. Поэтому если мы берём одинаковые тела, то плотность у них одинаковая. А если одно из тел по объёму больше, то да (при одинаковой плотности) в больший объём укладываются больше атомов и тело будет тяжелее (большее количество атомов участвуют в процессе). А вот утверждение, что тело с равной массой, но большего объёма — спорно (всё дело в том, что мы понимаем под определением массы тела). К примеру: согласно Вашей же статье «Почему не падают облака»- облако, состоящее из молекул воды, весом в 100 тонн — ни весит ничего, т.к. не падает и не может оказать давления на весы, а вот 100 тонн жидкой воды — очень даже весят. Так же и в вопросе: что больше весит — тонна железа или тонна дерева? Если вес тела это его реакция на краснофотонное излучение — это одно, но если мы под весом тела понимаем силу давления на площадку весов, то , да это другое. Здесь конечно нужно учитывать и вес столба воздуха над телом на эти же весы.
«Если вес тела это его реакция на краснофотонное излучение — это одно, но если мы под весом тела понимаем силу давления на площадку весов, то , да это другое».
—————————
НИ того, ни другого. Я зав складом, где на одном стеллаже лежит железо, а на втором дерево. Я тупо смотрю на шкалу весов, т.к. мне неведомы премудрости физиков с ихними красными или желтыми фотонами. Мне даже не интересно из чего состоят данные материалы, но зато передо мной одни весы и накладная, где написано: отпустить такому-то заказчику по одной тонне железа и дерева.
Накидал тонну железа на весы, штабелер погрузил в машину. Далее повторил то же самое с досками и не ошибся ни на один кг.
Относительно облаков. Тонна распылена в облаке. Мысленно приземлим это облако на те же весы и стрелка непременно отклонится на предполагаемое деление шкалы и будет равна тонне воды в бочке под потоком с крыши.